The p-value in statistics measures how strongly the data contradicts the null hypothesis.
A smaller p-value means the results are less consistent with the null and may support the alternative hypothesis. Common cutoffs for statistical significance are 0.05 and 0.01.
Key Takeaways
- Definition: A p-value measures how likely your observed results (or more extreme ones) would be if the null hypothesis were true. It is a tool for assessing evidence against the null.
- Significance: Statistical significance is determined by comparing the p-value to a chosen cutoff (often 0.05). A smaller p-value suggests stronger evidence against the null hypothesis.
- Misinterpretation: A p-value does not tell you the probability the null hypothesis is true or that your results happened by chance. It only reflects how your data aligns with the null model.
- Limitations: A statistically significant result may have little practical importance, and large samples can produce small p-values even for trivial effects. Always consider effect size and context.
- Best practice: Interpret p-values alongside confidence intervals, study design, and replication evidence to form a more reliable conclusion about your findings.
Hypothesis testing
When conducting a statistical test, the p-value helps determine whether your results are significant in relation to the null hypothesis.
The null hypothesis (H₀) states that no relationship exists between the variables being studied — in other words, one variable does not affect the other.
Under the null, any differences in results are attributed to chance, not to the factor you are investigating. Essentially, it assumes that the effect you are testing for does not exist.
The alternative hypothesis (H₁ or Hₐ) is the logical opposite.
It claims that the independent variable does influence the dependent variable, meaning the results are not purely due to random chance.
If the null hypothesis is rejected, the alternative becomes the more plausible explanation.
What a p-value tells you
A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).
The level of statistical significance is often expressed as a p-value between 0 and 1.
The smaller the p-value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.
Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true.
It’s a piece of evidence, not a definitive proof.
Example: Test Statistic and p-Value
Suppose you test whether a new drug provides more pain relief than a placebo.
If the drug has no real effect, your test statistic will be close to what’s expected under the null hypothesis, and the p-value will be high (close to 1).
If the drug truly works, your test statistic will differ more from the null expectation, and the p-value will drop.
A p-value never reaches exactly zero — there’s always a small possibility, however unlikely, that your observed results occurred by chance.
How to Choose an Alpha Level (significance threshold)
Your chosen alpha level (α) is the cutoff you use to decide whether results are statistically significant. The choice depends on your research context, goals, and the consequences of making a mistake.
-
Standard Alpha (α = .05): The most common threshold. Accepts a 5% chance of wrongly finding an effect that doesn’t exist (Type I error). Suitable for most exploratory or general research.
-
Stricter Alpha (α = .01 or .001): Used for high-stakes research, like clinical trials, mental health interventions, or policy decisions, where mistakes have serious consequences. A lower alpha reduces the chance of false positives (finding something significant that isn’t actually there).
-
Study Size and Reliability: Larger studies (typically 200 or more participants) often let you safely use a stricter alpha (e.g., α = .01), because larger samples provide more reliable results.
-
Practical Implications: If making a wrong decision could have major consequences (like health or safety risks), choose a lower alpha to minimize mistakes.
Always state and justify your chosen alpha level to increase transparency and trustworthiness.
P-value interpretation
The alpha level is a fixed threshold you set in advance; the p-value is calculated from your data. Comparing them tells you whether to reject the null hypothesis:
| P-value | Evidence against H₀ | Action |
|---|---|---|
| ≤ 0.01 | Very strong | Reject H₀ |
| ≤ 0.05 | Strong | Reject H₀ |
| > 0.05 | Weak or none | Fail to reject H₀ |
A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.
A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.
This suggests the effect under study likely represents a real relationship rather than just random chance.
For instance, if you set α = 0.05, you would reject the null hypothesis if your p-value ≤ 0.05.
It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).
Therefore, we reject the null hypothesis and accept the alternative hypothesis.
Example: Statistical Significance
Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05.
Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.
What does a p-value of 0.001 mean?
A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.
Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.
Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.
A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.
This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.
Note: when the p-value is above your threshold of significance, it does not mean that there is a 95% probability that the alternative hypothesis is true.
One-Tailed Test
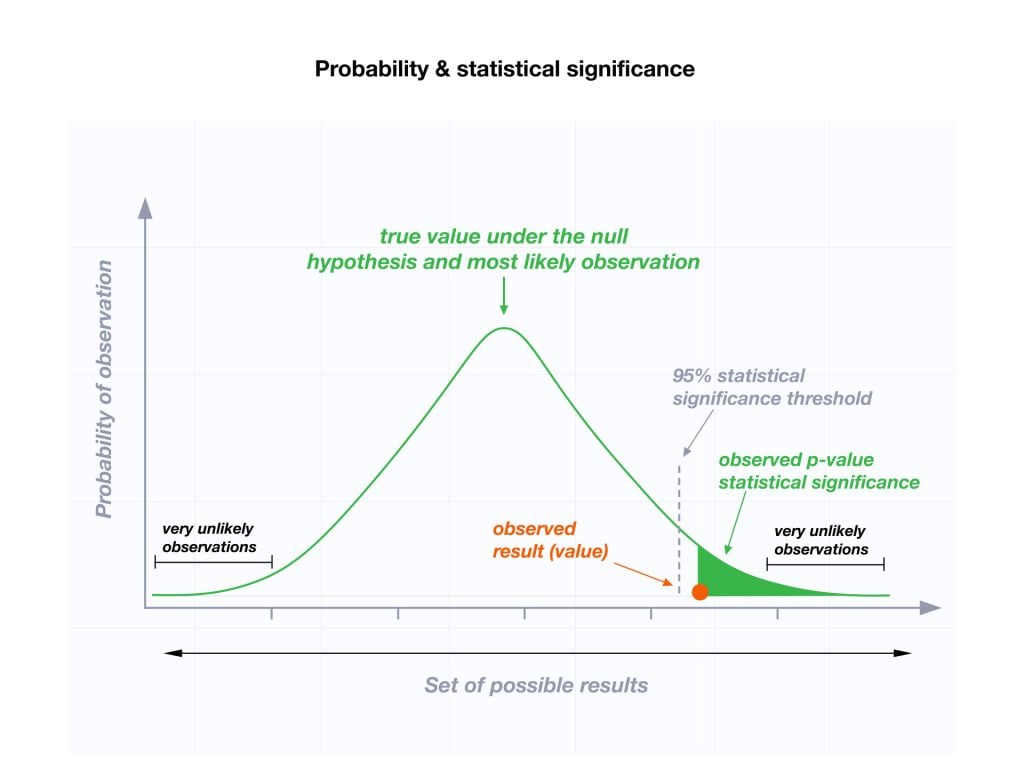
In a normal distribution, the significance level corresponds to extreme regions — or tails — of the curve.
In a one-tailed test, the entire significance level is assigned to one tail.
For example, with α = 0.05, you would reject the null hypothesis if your result falls in the extreme 5% region at one end of the distribution (either the right tail for a right-tailed test or the left tail for a left-tailed test).
If your observed value falls into this region (p ≤ 0.05), the null is rejected in favor of the alternative.
In this example, the observed value is statistically significant (p ≤ 0.05), so the null hypothesis (H0) is rejected, and the alternative hypothesis (Ha) is accepted.
Two-Tailed Test
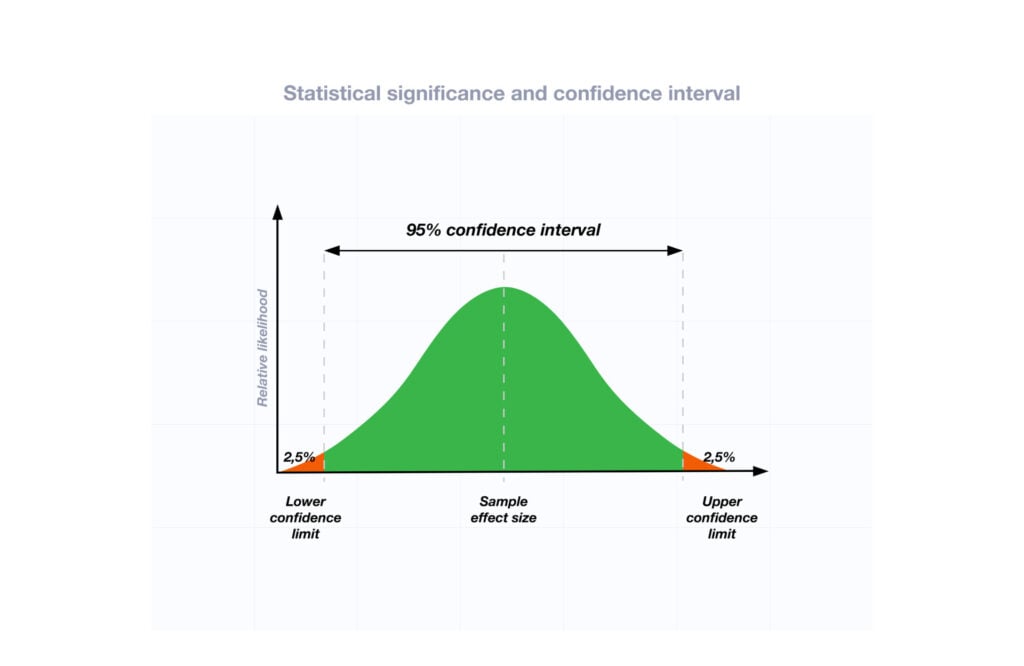
Two-tailed tests are used when an effect could occur in either direction, and they provide a more conservative test of significance.
In a two-tailed test, α is split equally between both ends of the normal distribution.
With α = 0.05, each tail contains 2.5% of the area under the curve.
Any data point landing in these extreme regions would be considered statistically significant at the 0.05 level, leading you to reject the null hypothesis.
Type I and Type II Errors
-
Type I Error (False Positive): This occurs when you incorrectly find an effect or difference that doesn’t really exist. For instance, concluding a medication improves symptoms when it actually does not. With an alpha (α) level of .05, there’s a 5% chance of making this error.
-
Type II Error (False Negative): This happens when you fail to detect an effect that genuinely exists. For example, concluding a medication doesn’t help when it truly does. You can reduce this error by increasing your sample size or improving your research design.
How do you calculate the p-value?
Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.
You can also estimate a p-value using online calculators or statistical tables, which require your test statistic and degrees of freedom.
These tables show how often you’d expect to see your test statistic if the null hypothesis were true.
Understanding the Statistical Test:
Choosing the right statistical test matters because each has its own purpose and assumptions:
-
T-test: Compares the means of two groups (e.g., testing if one medication is more effective than another).
-
ANOVA (Analysis of Variance). Compares means across three or more groups (e.g., therapy, medication, and combined treatment).
-
Chi-squared test: Suitable for categorical data (e.g., evaluating the relationship between smoking status and lung disease).
-
Correlation test: Measures the strength and direction of relationships between two continuous variables (e.g., height and weight).
Example: Choosing a Statistical Test
The more variables you include, the more careful you must be interpreting your p-values.
More variables can affect your test statistic, potentially leading to misleading significance.
If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance (ANOVA).
Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.
How to report
A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).
Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).
Example: Reporting the results
In our comparison of pain relief between the new drug and a placebo, participants in the drug group reported significantly lower pain scores (M = 3.5, SD = 0.8) than those in the placebo group (M = 5.2, SD = 0.7). This 1.7-point difference on the pain scale was statistically significant, t(98) = -9.36, p < .001.
APA Style
The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:
“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.
The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)
Note:
- Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
- Please pay attention to issues of italics (p is always italicized) and spacing (either side of the = sign).
- p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
- The opposite of significant is “nonsignificant,” not “insignificant.”
Statistical vs. practical significance
A common mistake is to assume that a lower p-value means a stronger relationship or a more important finding.
In reality, a p-value only tells you how unlikely your data would be if the null hypothesis were true. It does not reveal the size or real-world importance of the effect.
- Statistical significance means the evidence is strong enough to reject the null hypothesis at a chosen threshold (e.g., p < 0.05).
- Practical significance, on the other hand, considers whether the effect is big enough to make a real difference in everyday life, not just in a statistical test.
This is often measured with effect size, which quantifies the magnitude of the difference or relationship.
| Statistical Significance | Practical Significance | |
|---|---|---|
| Definition | Indicates the data provide enough evidence to reject the null hypothesis at a chosen p-value threshold. | Assesses whether the size of the effect is large enough to matter in real-world or applied contexts. |
| Measure | p-value (compared to α, e.g., 0.05). | Effect size (e.g., Cohen’s d, correlation coefficient) and real-world impact. |
| Tells You | Whether the result is likely due to more than random chance. | Whether the effect is meaningful or valuable in practice. |
| Example | p = 0.02 suggests strong evidence against the null. | A new diet might cause just half a pound of weight loss in three months — statistically significant, but too small effect to matter for most people. |
| Limitation | Says nothing about the magnitude or importance of the effect. | May overlook results that are statistically weak but still important in specific contexts. |
Relationship Between Effect Size, Confidence Intervals, and P-Values
Effect size, confidence intervals, and p-values each contribute uniquely and complementarily to statistical interpretation:
-
Effect Size: Measures how large or meaningful the effect is. For example, a therapy may significantly reduce anxiety scores, but if the change is only 1–2 points on a 50-point scale, the practical impact is minimal.
-
Confidence Intervals (CIs): Give a range of values in which the true effect likely lies (often 95% CIs). Narrow intervals suggest more precise estimates; wide intervals indicate greater uncertainty.
-
P-Values: Reflect statistical significance, not practical value.
For example, a very small p-value (such as 0.001) in a depression intervention trial suggests strong statistical evidence that the intervention had some effect, but without effect size, it doesn’t indicate if the change is clinically meaningful.
Combining These Concepts:
- Small p-value + Large effect size + Narrow CI: Strong evidence that the effect is real and practically significant.
- Small p-value + Small effect size: Indicates statistical significance, but the practical impact may be limited.
- Significant p-value + Wide CI: Suggests uncertainty about the exact size of the effect, indicating caution in interpreting results.
Reporting effect sizes, confidence intervals, and p-values together ensures thorough, transparent, and meaningful interpretation of your research findings.
Multiple comparisons & p-hacking
When researchers run many statistical tests on the same dataset, the chance of finding a “significant” result purely by luck increases.
This is called the multiple comparisons problem.
For example, if you test 20 unrelated hypotheses at the usual α = 0.05 threshold, you can expect about one false positive result just by chance.
P-hacking happens when researchers — intentionally or not — run many analyses, report only the significant results, or stop collecting data once they get the outcome they want.
This can make an effect seem real when it’s actually just a statistical fluke.
To avoid these pitfalls, researchers can:
-
Pre-register their hypotheses and analysis plans before collecting data.
-
Use adjustments for multiple testing, such as the Bonferroni correction, to keep the overall error rate under control.
-
Report all analyses conducted, not just the ones that turned out significant.
The bottom line: statistical significance is most trustworthy when the analysis plan is transparent, limited to the main research questions, and adjusted for the number of tests performed.
FAQs
When do you reject the null hypothesis?
In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test.
The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.
Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.
The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.
What does p-value of 0.05 mean?
If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant.
This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.
Are all p-values below 0.05 considered statistically significant?
No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention.
Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.
A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.
Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.
How does sample size affect the interpretation of p-values?
Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.
With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values.
In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.
Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.
Can a non-significant p-value indicate that there is no effect or difference in the data?
No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.
There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.
Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.
Can P values be exactly zero?
While a p-value can be extremely small, it cannot technically be absolute zero.
When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001
My experiment yielded a p-value of 0.06. Should I discard my hypothesis entirely? How should I interpret this result accurately?
A p-value of 0.06 means there’s only a 6% chance your results would occur if there’s truly no effect—still relatively low.
Being close to significance might suggest there could be an effect, but your evidence isn’t strong enough yet.
You might have encountered a Type II error (failing to detect a real effect).
If your sample size is small or your study has low statistical power (below 80%), you may have missed detecting an actual effect.
Look at the effect size: is it meaningful enough to matter in real-world scenarios?
A practically significant effect could still be important, even without statistical significance.
If your confidence interval is narrow and mostly suggests a meaningful effect, this increases confidence that the result may still have practical value.
A wide interval suggests greater uncertainty, making conclusions less reliable.
Assess if there were methodological limitations or biases (like measurement error or uncontrolled variables) that may have weakened your results.
Check if other research supports similar findings or trends. If consistent with existing literature, your result could still be meaningful.
Can p-values be manipulated or misleading?
Yes. P-values can be misleading if researchers engage in practices like p-hacking – repeating analyses, selectively reporting results, or stopping data collection once significance is reached.
They can also appear small in very large samples even for trivial effects, so context and additional statistics are essential.
What happens if results are significant in one study but not in another?
When one study finds a significant result and another does not, it usually means the evidence is mixed rather than one study “proving” and the other “disproving” the effect.
Differences in sample size, study design, measurement precision, and random variation can explain the discrepancy.
Looking at the effect sizes, confidence intervals, and results from multiple studies (meta-analysis) is the best way to judge the overall evidence.
Further Information
- P Value Calculator From T Score
- P-Value Calculator For Chi-Square
- P-values and significance tests (Kahn Academy)
- Hypothesis testing and p-values (Kahn Academy)
- Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
- Criticism of using the “ p “< 0.05”.
- Publication manual of the American Psychological Association
- Statistics for Psychology Book Download
Sources:
Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply. BMJ: British Medical Journal, 309(6958), 874.
Goodman, S. N., & Royall, R. (1988). Evidence and scientific research. American Journal of Public Health, 78(12), 1568-1574.
Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions. In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.
Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value. Epidemiology (Cambridge, Mass.), 9(1), 7-8.


